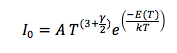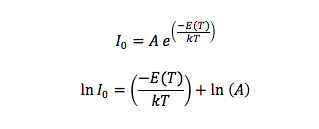In this experiment, I investigated the current-voltage relationship of a p-n junction at different temperatures. A p-n junction is a boundary between two types of semiconductor material, p-type and n-type. A p-type semiconductor has excess holes, where a hole is the absence of an electron. While an n-type semiconductor has excess electrons.

Therefore, if we measure current as a function of voltage, we will be able to find Io and e/(kT). Note that the ratio e/k is , the charge of the electron over the boltzmann’s constant, which is a constant that relates energy at an individual particle level to temperature.

The apparatus consisted of a dc voltage source that was built from a 1Ω helipot and a 1.5 battery. This was connected to a picoammeter, Keithey Model 480, which measured the current in the circuit. The circuit also contained an n-p-n transistor which was exposed to various temperatures.

We placed the transistor and a thermometer in a tube with oil and measured at room temperature (293 Kelvin) the current as we varied the voltage. We then placed the tube in a water/ ice mixture with a temperature of 274.3 Kelvin and measured the current. Afterwards we placed the tube in boiling water, whose temperature was 370.2 Kevin. We then removed the transistor from the tube with oil and placed it in a container where we also placed dry ice and Isopropyl Alcohol. We also measured the temperature that the transistor was exposed to, which was 197.5 Kelvin. Finally we placed the transistor and thermometer in a vat containing liquid nitrogen (82.2 Kelvin) and measured the current as a function of voltage.

Current vs Voltage for various temperatures (82.2, 197.5, 274.3, 293, 370.2 Kelvin.) Observe that as the temperature increases, the voltage values decrease. On the other hand the slope of the linear fits increases as the temperature decreases.

From the linear fit of the data for each linear fit I found the ratio e/k and Io; because e/k was the slope of line and Io was the y-intercept. I calculated e/kT from the known e, K and T values and compared it to the slopes of the linear fits for each temperature T. I discovered that all of my slopes where within error of the calculated ratio. Therefore the y-intercept values which corresponded to Io would also be within error.

a) Representative data of the e/kT ratio. Note that the calculated values where within error of the measured values.
b) Representative data of the ln(I_0) values for each temperature (I made a mistake when writing the tables, I_o should be ln(I_0).) Unlike the e/k ratio it does depend on the temperature and we do not have a way to calculate it because it depends on the band gap energy of the semiconductor.

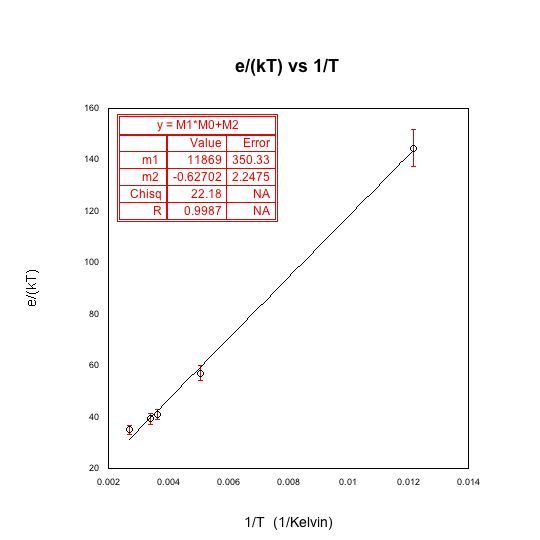
Plot of e/(kT) vs 1/T, where e/(kT) values were obtained from the line fit of current vs voltage. The fact that these values fit a straight lines tells us that e/k is constant as it should be. We can conclude, from the fit, that e/k is equal to 11869 plus or minus 350.33 Kelvin.

Finally, I measured the band gap energy, which in the case of semiconductors is the range of energy between the valence band and the conduction band. The valence band is the energy range, where the electrons are localized and not allowed to moved, and the conduction band is the energy values necessary for the electrons to be freed from the valence band and conduct energy. From the literature, I knew that:

where A is constant, E(T) is the band gap energy, which is time dependent, and γ is a constant that depends on the temperature dependence of the mobility, lifetime and diffusion coefficient of minority carriers. Semiconductors have majority and minority carriers, if the semiconductor material is p-type then the majority carriers are holes and the minority carriers are electrons, and vice versa for n-type semiconductors. Although majority carriers are primarily responsible for current transport, minority carriers are also important in how current runs through the material, especially if it is a p-n junction. In any case, we can simplify the equation if we consider that the exponential term will increase much faster than the the function T^(3+γ/2). Then, we do not have to worry about the minority carriers and we solve for the band gap energy and we will consider E(T) to be constant.

I plotted the ratio 1/T vs the natural logarithm of each  Io value, because the slope of the resulting line would equal E(T)/k and the y-intercept would equal ln(A). We found that E(T)/k=14534 ± 166.15 Kelvin, and since k=8.617 x10^(-5) eV/Kelvin, E(T)=1.2523 ± 0.1432 eV. This value of the band gap energy for a p-n junction was slightly higher than the value in the literature, which was 1.11-1.13 eV. This discrepancy can be explained by the fact that we simplified the equation for Io and did not take into account minority carriers.

Plot of e/(kT) vs 1/T, where e/(kT) values were obtained from the line fit of current vs voltage. The fact that these values fit a straight lines tells us that e/k is constant as it should be. We can conclude, from the fit, that e/k is equal to 11869 plus or minus 350.33 Kelvin.

In the end we measured the ratio e/k and the band gap energy of a p-n junction and both values where within error and their uncertainty was probably due to the generalizations in the equations. This was a really fun lab because I got to use liquid nitrogen and dry ice, and because collecting data was fairly painless and quick.