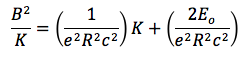In this experiment I measured the maximum kinetic energy  of a source that emits beta particles and is experiencing a magnetic force.

Beta decay occurs when an atom has too many neutrons or protons and one decays into the other. This decay results in the emission of a neutrino and either a positron or electron. Beta decay was the first clue to the existence of the neutrino. The neutrino was needed to account for the loss of energy and momentum that was measured from the emitted particles.

I had a detector inside a brass chamber, where we could place the source perpendicularly to the detector or right in front of it. The detector measured the electrons emitted by the source  This chamber was connected to a Preamplifier, and to a Voltage supply so that we could create a current within the chamber.

The output pulse of the detector went though the preamp, an amplifier and an oscilloscope before going into the CANBERRA Series 35 Plus. The Canberra collected the data and created a histogram of channel number vs counts, where the channel number was proportional to the energy of the pulse.

Note how the source can be placed directly in front of the detector or 180 degrees away from it. Also note that we use slits to define the radius of curvature of the beta rays emitted by the source.

In order to determine the relationship between the channel numbers and the energy values, I measured the known maximum kinetic energies (KEmax) of the sources. I found a spectra for Srontium, Chlorine-36, Thalium-204 and Technetium-99 and measured the channel where KEmax occurred.

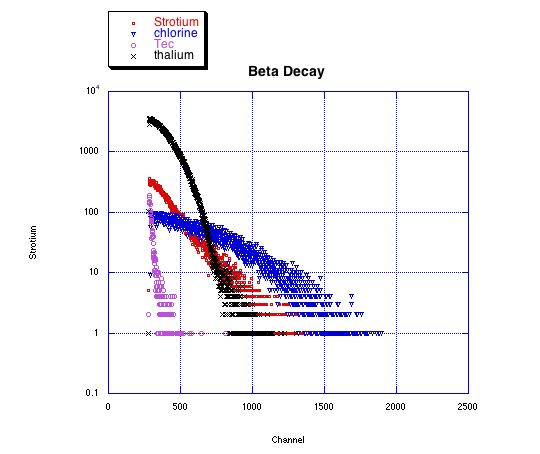
The thalium had a smaller maximum Kinetic Energy than the strontium and the chlorine, which was not what we had expected given their known maximum kinetic energies.

The known KEmax (763 keV) of Thalium is bigger than that of chlorine (708 keV) and strontium (546 keV). Since I measured it as smaller than the KEmax of chlorine and strontium I had to discard it for my calibration line.

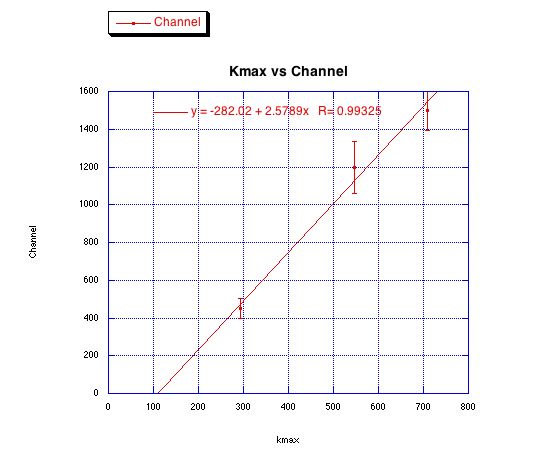
I only used our data from the strotium, chlorine and techerium sources. I discarded the thalium source data because the measured KEmax was smaller than we expected.

I proceeded to measure the Energy of chlorine-36 in different magnetic fields. I placed the source 180 degrees away from the detector and evacuated the chamber. Then, I placed it between the two magnets. A current was fed into the magnets by the   which produced a magnetic field that was constant in the radial direction of the chamber. I measured the strength of the magnetic field within the chamber with a gaussmeter. I measured the source’s energy peak as a function of current. As I was doing this the CANBERRA died, and I lost two of my spectra.

I measured the energy peaks from the data I hadn’t lost and graphed it vs the magnetic field I had measured squared over the kinetic energy. I only used three data points since I lost the rest. On the other hand, the line is within error. The line had a slope of -68.487 and an intercept of 2.8512.

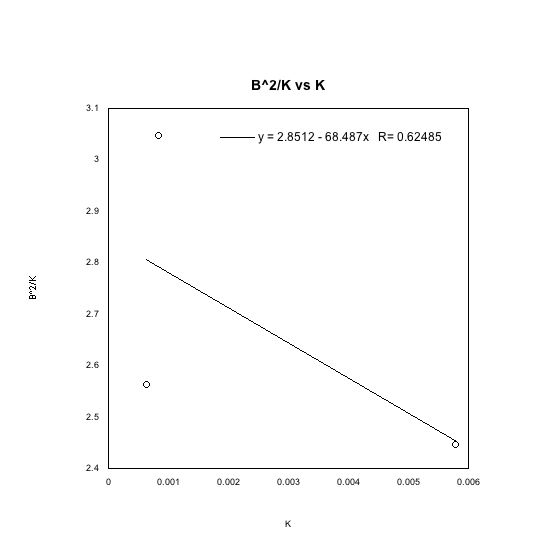
I plotted B^2/K vs K in order to calculate the charge of the electron and the rest energy of the electron E_0. Unfortunately my data did not fit a line well, and the uncertainty is of the fitted line is very high. This uncertainty is due to the uncertainty of the energy calibration and to the fact that there was very little data to work from.

The line I found corresponded to the following equation. As a result we can find the charge of the electron and the rest energy E_0.

This equation is derived in the lab write-up

 I calculated the electron charge to be e=1 x 10 ^(-8) C, which was not within error of the standard value, e=-1.6021765 x10^(-19) C. The rest energy, which depended on e, was equal to 3.311 x10^(-4) joules. From this we can find the electrons rest mass because E_0=m c^2, where m is the electrons rest mass. The rest mass is equal to 3.6788 x10^(11) kg which was still very different from the standard value 9.109×10^(-31) kg. The gigantic uncertainty of these values is due to various factors, firstly the energy calibrations uncertainty. It is also due to the uncertainty in measuring the peak of the data and determining K. Furthermore, I lost data and I cannot determine whether any of the three point can or cannot be discarded.